Question

An archer shoots an arrow toward a 300-g target that is sliding in her direction at a speed of 2.40 m/s on a smooth, slippery surface. the 22.5-g arrow is shot with a speed of 38.5 m/s and passes through the target, which is stopped by the impact. what is the speed of the arrow after passing through the target?

Answer 1

The speed of the arrow after passing through the target is 6.5 m/s

Step-by-step explanation:

Given that,

Mass of target = 300 g

Speed of target = 2.40 m/s

Mass of arrow = 22.5 g

Speed of arrow = 38.5 m/s

After impact the momentum of the target is zero since its velocity is zero.

After impact the velocity of the arrow can be determined with conservation of momentum

`\Delta p_(a)=-\Delta p_(t)`

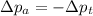
We need to calculate the speed of the arrow after passing through the target

Using conservation of momentum

`m_(a)v_(a)_(i)+m_(t)v_(t)_(i)=-m_(a)v_(a)_(f)-m_(t)v_(t)_(f)`

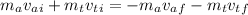
Put the value into the formula

`0.0225*38.5-0.3*2.40=- 0.0225* v_(f)-0`

`v_(f)=(0.0225*38.5-0.3*2.40)/(-0.0225)`

`v_(f)=6.5\ m/s`

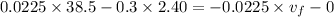
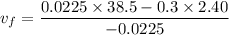
Hence,The speed of the arrow after passing through the target is 6.5 m/s

Answer 2

6.5 m/s
An object's momentum is its speed (m/s) multiplied by its mass(kg).
initial momentum of target = 0.3kg x 2.4m/s = 0.72
initial momentum of arrow = 0.0225kg x 38.5m/s = 0.86625
resulting momentum of arrow is 0.86625 - 0.72 = 0.14625
momentum /mass = speed
so 0.14625 /0.0225 = 6.5 m/s