Question

Which of the following statements have the same result? Explain each step in solving each one.

I. f(2) when f(x) = 3x + 2
II. f−1(3) when f(x) = 2 x minus 7, all over 3
III. 2y + 14 = 4y − 2

Answer 1

I. f(2) when f(x) = 3x + 2
f(2) = 3(2) + 2=8
III. 2y + 14 = 4y − 2
4y- 2y = 14+2
2y = 16
y=16/2=8
statements have the same result

Answer 2

All three statements have same results.

Explanation:

Statement I: f(2) when f(x) = 3x + 2.

`f(x)=3x+2`

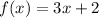
Put x=2.

`f(x)=3(2)+2=8`

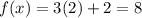
The value of the function is 8. It means y=8 at x=2.

Statement II:f⁻¹(3). when f(x) = 2 x minus 7, all over 3.

`f(x)=(2x-7)/(3)`

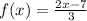
Find the inverse of the function.

Step 1: Substitute f(x)=y

`y=(2x-7)/(3)`

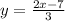
Step 2: Interchange x and y.

`x=(2y-7)/(3)`

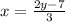
Step 3: Isolate y.

`y=(3x+7)/(2)`

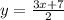
Step 4: Substitute y=f⁻¹(x).

`f^(-1)(x)=(3x+7)/(2)`

Now, substitute x=3, to find f⁻¹(3).

`f^(-1)(3)=(3(3)+7)/(2)=8`

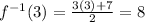
The result of statement II is 8.

Statement III: 2y + 14 = 4y − 2

`2y+14=4y-2`

`14+2=4y-2y`

`16=2y`

`y=8`

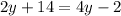
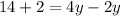
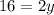
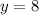
The result of statement III is 8.

Therefore all three statements have same results.