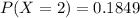Question

In each of the months June, July, and August, the number of accidents occurring in that month is modeled by a Poisson random variable with mean 1. In each of the other 9 months of the year, the number of accidents occurring is modeled by a Poisson random variable with mean 0.5. Assume that these 12 random variables are mutually independent. Calculate the probability that exactly two accidents occur in July through Novembe

Answer 1

`P(X=2)=0.1849`

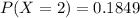
Explanation:

From the question we are told that

Sample size n=3

Sample mean 1
`\=x_1=1`

Sample mean 2
`\=x_2=0.5`

Generally the Probability that 2 accidents occurs from July to August is mathematically given by

`mean\ accidents=2*\=x_1`

`mean\ accidents=2*1`

`mean\ accidents=2`

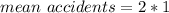
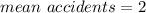
Generally the probability that 2 deaths occurs from September through November is mathematically given by

`Mean\ accidents=3*\=x_2`

`Mean\ accidents=3*0.5`

`Mean\ accidents=1.5`

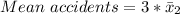
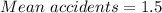
Therefore

Total Mean accidents
`T_a=2+1.5=>3.5`

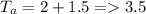
Generally the probability of two accident per month is mathematically given by

`P(X=2)=(e^-^3^.^5*3.5^2)/(2!)`

`P(X=2)=0.1849`

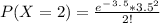
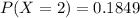
Therefore the probability of having 2 accidents from July through to November is

`P(X=2)=0.1849`