Question

Identify the vertex for the graph of y = 2x2 + 8x − 3. (2, 21) (2, 17) (−2, −11) (−2, −27)

Answer 1

`\bf \textit{vertex of a vertical parabola, using coefficients} \\\\ \begin{array}{lcccl} y = & 2x^2& +8x& -3\\ &\uparrow &\uparrow &\uparrow \\ &a&b&c \end{array} \qquad \left(-\cfrac{ b}{2 a}\quad ,\quad c-\cfrac{ b^2}{4 a}\right) \\\\\\ \left( -\cfrac{8}{2(2)}~~,~~-3-\cfrac{8^2}{4(2)} \right)\implies \left( \cfrac{-8}{4}~~,~~-3-\cfrac{64}{8} \right) \\\\\\ \left(-2~~,~~-3-8 \right)\implies (-2~~,~~-11)`

Answer 2

The vertex is (-2, -11 ).

Explanation:

Here, the given equation is,

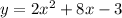`y = 2x^2 + 8x - 3` -----(1)

Which is a parabola along x-axis,

Since, the standard form of parabola along x-axis is,

`y=a(x-h)^2 + k`

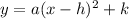
Where (h,k) is the vertex of the parabola,

By solving it,

`y = ax^2 - 2ahx + ah^2 + k` -----(2),

By comparing equation (1) and (2),

We get,

a = 2, -2ah = 8 and ah² + k = - 3

⇒ -2(2) h = 8 ⇒ - 4 h = 8 ⇒ h = -2

And, (2)(-2)² + k = - 3

⇒ 8 + k = - 3

⇒ k = -11

Hence, the vertex of the given equation is (-2, -11 )