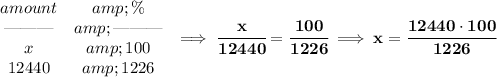let's say there were "x" in 1996, therefore, "x" is the 100%.
10 years later, there are 12440, and that is 1126% "more" than "x", since "x" is 100%, 1126% more than that is 100% + 1126%, or 1226%.
so, 12440 is really 1226% of whatever "x" happened to have been back then in 1996.
now, since we know that 12440 is 1226%, what is "x" then?