Question

If sin theta = -5/7 , which of the following are possible?

A) cos theta = √24/7 , and tan theta = 5/√24
B) cos theta = -√24/7, and tan theta = 5/√24
C) sec theta = 7/√24 , and tan theta = -5/√24
D)sec theta = -7/5, and tan theta = 5/√24

Answer 1

It is given that

`sin \theta = (-5)/(7)`

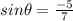
And according to pythagorean identity, we will get

`cos \theta = \pm √(1-sin^2 \theta)`

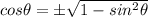
Substituting the value of sin theta, we will get

`cos \theta = \pm \sqrt{1- (25)/(49)} \\ cos \theta = \pm (√(24))/(7)`

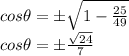
and sec theta is the reciprocal of cos theta.

SO possible values of sec theta are

`sec \theta = \pm (7)/( √(24))`

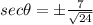
And tan theta is the ratio of sin theta and cos theta

So possible values of tan theta are

`tan  \theta = \pm (5)/( √(24))`

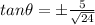
So the correct options are B and C .

Answer 2

we are given that

`sin \theta=-5/7`

As we know that

`cos \theta =√(1-sin^2 \theta)  \\`

Substitute the value we get

`cos \theta=\sqrt{1-((-5)/(7))^2}  \\ \\ cos \theta=\sqrt{1-((25)/(49))}  \\ \\ cos \theta=\sqrt{((24)/(49))} =(√(24))/(7)\\`

Since
`sec \theta=(1)/(cos \theta)\\`

So here
`sec \theta=(7)/(√(24))\\`

As we know that

`tan \theta=(sin \theta)/(cos \theta)\\ \\  \text{Substitute the values we get}\\ \\ tan \theta=(-5/7)/((√(24))/(7))\\ \\ tan \theta=(-5)/(√(24))\\`

Hence the correct option is C.