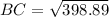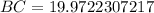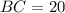Answer:
Angles:
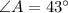

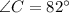
Sides:
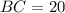
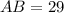
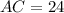
Explanation:
See attachment for complete question
From the attachment, we have:
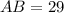
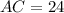
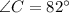
Required
Complete the missing side and missing angles
To calculate angle B, we apply sine laws:
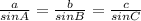
In this case:
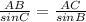
This gives:
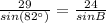
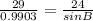
Cross Multiply
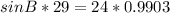
Divide both sides by 29
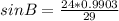
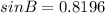
Take arcsin of both sides
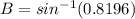
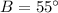
So:

To solve for the third angle, we make use of:
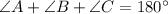
This gives:
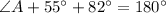
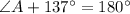
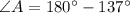
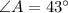
Hence, the angles are:
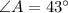

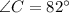
To calculate the length of the third side, we apply cosine law

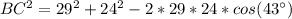


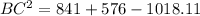
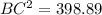
Take the square root of both sides