Question

A survey found that 31 of 60 randomly selected women and 38 of 73 randomly selected men follow a regular exercise program. Find a 95% confidence interval for the difference between the proportions of women and men who follow a regular exercise program.

Answer 1

95% confidence interval for the difference between the proportions of women and men who follow a regular exercise program

(-0.1740 , 0.1672)

Explanation:

Step(i):-

Given A survey found that 31 of 60 randomly selected women

First sample proportion

`p_(1) = (x_(1) )/(n_(1) ) = (31)/(60) = 0.5166`

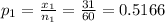
Second sample proportion

`p_(2) = (x_(2) )/(n_(2) ) = (38)/(73) = 0.520`

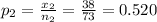
Level of significance = 0.05

Z₀.₀₅ = 1.96

Step(ii):-

95% confidence interval for the difference between the proportions of women and men who follow a regular exercise program

`((p_(1) ^(-)-p^(-) _(2) - Z_(0.05) S.E(p_(1) ^(-) - p^(-) _(2) ), (p_(1) ^(-)-p^(-) _(2) +Z_(0.05) S.E(p_(1) ^(-) - p^(-) _(2) ))`

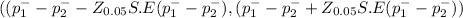
where

`Se(p_(1) - p_(2) ) = \sqrt{(p_(1) (1-p_(1) ))/(n_(1) )+(p_(2)(1-p_(2) )/(n_(2) ) }`

`Se(p_(1) - p_(2) ) = \sqrt{(0.5166 (1-0.5166 ))/(60 )+(0.520(1-0.520 )/(73 ) } = 0.08706`

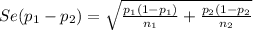
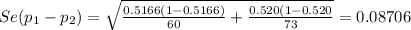
95% confidence interval for the difference between the proportions of women and men who follow a regular exercise program

`((p_(1) ^(-)-p^(-) _(2) - Z_(0.05) S.E(p_(1) ^(-) - p^(-) _(2) ), (p_(1) ^(-)-p^(-) _(2) +Z_(0.05) S.E(p_(1) ^(-) - p^(-) _(2) ))`

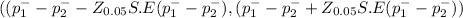
((0.5166-0.520-1.96(0.08706) , 0.5166-0.520+1.96(0.08706))

(-0.1740 , 0.1672)

Final answer:-

95% confidence interval for the difference between the proportions of women and men who follow a regular exercise program

(-0.1740 , 0.1672)