Question

A bin of 50 parts contains 5 that are defective. a sample of 10 parts is selected at random, without replacement. how many samples contain at least four defective parts.

Answer 1

FROM the 5 defective parts , select 4, and the number of ways to complete this step (5!/4!1!) =5 . from the 45 non-defective parts ,select 6, and the number of ways to complete this step 45!/(6!39!) =8,145,060. THEREFORE the number of samples that contain exactly 4 defective parts is 5(8,145,060 )= 40,725,300 , the number of ways to select 5 is 5!(5!1!)=1. from the 45 non-defective parts select 5 and the numbers of ways to complete this step is 45!/(5!40!)=1221759 . therefore the number of samples that contain exactly 5 defective parts is 1(1221759)=41947059. therefore ,the number of samples that contain exactly 5 defective parts is 1(1221759) =1221759 . therefore the number of samples that contain at least four defective parts is 40725300+1221759=41947059

Answer 2

41,947,059 samples contain at least four defective parts.

Explanation:

The order of the parts are not important, and they are chosen without replacement. So the combinations formula is used to solve this question.

Combinations formula:

`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

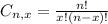
4 defective parts:

There are 10 parts chosen, of 50 in total.

We want 4 defective, from a set of 5.

And 10-4 = 6 non-defective, from a set of 50-5 = 45. So

`C_(5,4)*C_(45,6) = (5!)/(4!(5-4!))*(45!)/(6!(45-6!)) = 40725300`

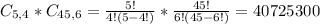
5 defective parts:

5 defective, from a set of 5.

5 non-defective, from a set of 45. So

`C_(5,5)*C_(45,5) = (5!)/(5!(5-5!))*(45!)/(5!(45-5!)) = 1221759`

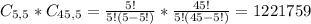
How many samples contain at least four defective parts.

40725300 + 1221759 = 41,947,059

41,947,059 contain at least four defective parts.