Question

A mass of 1.5 kg is attached to a spring and placed on a horizontal surface. The spring has a spring constant of 120 N/m, and the spring is compressed 0.25 m past its natural length. If the mass is released from this compressed position, what is the speed of the mass as it passes the natural length of the spring? A. 3.4 m/s B. 1.5 m/s C. 0.99 m/s D. 2.2 m/s

Answer 1

Answer: 2.2

Step-by-step explanation:

Answer 2

Speed of the mass is 2.2 m/s

Step-by-step explanation:

It is given that,

Mass of the object, m = 1.5 kg

Spring constant of the spring, k = 120 N/m

The spring is compressed by a distance of, x = 0.25 m

The mass is released from this compressed position, then the initial kinetic energy of block is equal to the spring potential energy i.e.

`(1)/(2)kx^2=(1)/(2)mv^2`

v is the speed of the mass.

`v=\sqrt{(kx^2)/(m)}`

`v=\sqrt{(120* (0.25)^2)/(1.5)}`

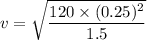
v = 2.23 m/s

The speed of the mass as it passes the natural length of the spring is 2.2 m/s. Hence, the correct option is (d).