Question

Determine which polynomial can be rewritten to include the factor below.

(x -7 + 11i)
A. x2 - 14x + 170
B. x2 - 7x + 170
C. x2 - 7x + 121
D. x2 - 14x + 121

Answer 1

Option A -
`x^2-14x+170=0`

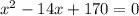
Explanation:

Given : The factor
`(x-7+11i)`

To find : Determine which polynomial can be rewritten to include the factor below?

Solution :

A quadratic equation
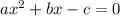`ax^2+bx-c=0` in which
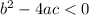`b^2-4ac<0` has two complex roots
`x=(-b+i√(b^2-4ac))/(2a),(-b-i√(b^2-4ac))/(2a)`

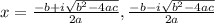
So, There always exist a root with positive i and negative i.

So, one root of the polynomial is
`(x-7+11i)` then the other root must be
`(x-7-11i)`

Now, We have two roots so multiply them to find the polynomial.

`(x-7+11i)(x-7-11i)=0`

`x^2-7x-11ix-7x+49+77i+11ix-77i-(11i)^2=0`

`x^2-14x+49-121i^2=0`

`x^2-14x+49+121=0`

`x^2-14x+170=0`

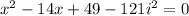
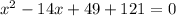
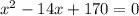
Therefore, Option A is correct.