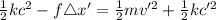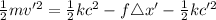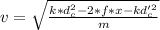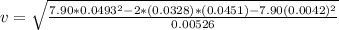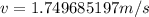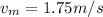Answer:
a)
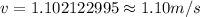
b)
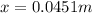
c)
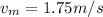
Step-by-step explanation:
From the question we are told that
Mass of soft rubber
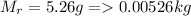
Spring compression
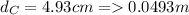
Stiffness constant
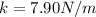
Ball Distance
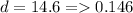
Frictional force
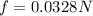
a)Generally the equation for motion of the second ball according to Newton's law is given by
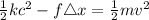
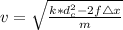
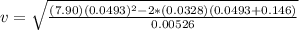
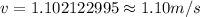
b)Generally for speed to be at maximum spring force must equal frictional force
At distance
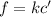
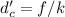
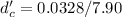
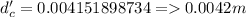
Therefore
Ball is at maximum speed at
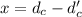
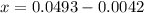
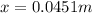
c)Generally maximum velocity is represented mathematically as