Question

Use Euler’s Formula to find the number of vertices in a polyhedron with four triangular faces.

Answer 1

`V=4`

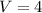
Explanation:

we know that

The Euler's formula state that, the number of vertices, minus the number of edges, plus the number of faces, is equal to two

Let

V----> the number of vertices

E------> the number of edges

F------> the number of faces

`V - E + F = 2`

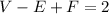
In this problem we have

`F=4, E=6`

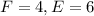
substitute in the formula and solve for V

`V-6+4 = 2`

`V-6+4 = 2`

`V=4`

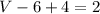
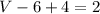
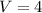
see the attached figure to better understand the problem

Answer 2

Euler formula:

`V-E+F=2`
Since
`F=4` then

`V-E+4=2\\V-E=-2\\V=E-2` and
`E=8` (check the figure)
So:

`V=8-4=4` is the number of vertices.