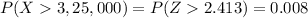Question

The distribution of prices for home sales in a certain New Jersey county is skewed to the right with a mean of $290,000 and a standard deviation of $145,000. Suppose Mrs. McCann selects a simple random sample of 100 home sales from this (very large) population. What is the probability that the mean of the sample is greater than $325,000

Answer 1

The probability that the mean of the sample is greater than $325,000

`P( X > 3,25,000) = P( Z >2.413) = 0.008`

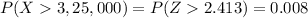
Explanation:

Step(i):-

Given the mean of the Population( )= $290,000

Standard deviation of the Population = $145,000

Given the size of the sample 'n' = 100

Given 'X⁻' be a random variable in Normal distribution

Let X⁻ = 325,000

`Z = (x^(-)-mean )/((S.D)/(√(n) ) ) = (325000-290000)/((145000)/(√(100) ) ) = 2.413`

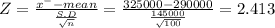
Step(ii):-

The probability that the mean of the sample is greater than $325,000

`P( X > 3,25,000) = P( Z >2.413)`

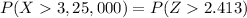
= 0.5 - A(2.413)

= 0.5 - 0.4920

= 0.008

Final answer:-

The probability that the mean of the sample is greater than $325,000

`P( X > 3,25,000) = P( Z >2.413) = 0.008`