Answer:
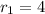 ω
ω
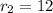 ω
ω
Explanation:
The Student is able to obtain four values of resistances using only two resistors
 and
and
 , like that:
, like that:
1. Resistance with a value of
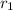
2. Resistance with a value of
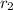
3. Resistance making series with
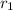 and
and
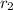
4. Resistance making a parallel with
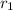 and
and
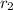
You know that the value of resistance in series is defined by the sum of each one of them, in this case as shown below:
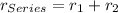
Now, we´ll combine in pair every value of resistance given in the statement using the formula for resistance in series and in this way to know the values for
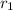 and
and
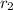 .
.
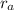 = 3 ω + 4 ω =>
= 3 ω + 4 ω =>
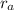 = 7 ω
= 7 ω
 = 3 ω + 12 ω =>
= 3 ω + 12 ω =>
 = 15 ω
= 15 ω
 = 3 ω + 16 ω =>
= 3 ω + 16 ω =>
 = 19 ω
= 19 ω
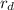 = 4 ω + 12 ω =>
= 4 ω + 12 ω =>
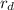 = 16 ω
= 16 ω
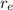 = 12 ω + 16 ω =>
= 12 ω + 16 ω =>
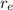 = 28 ω
= 28 ω
If you realize, the results of resistance from what we called
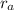 ,
,
 ,
,
 and
and
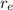 not corresponding with the values in the statement, but
not corresponding with the values in the statement, but
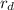 does.
does.
So you guess that
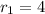 ω and
ω and
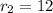 ω, but you must meet the condition, resistance in parallel be equal to 3 ω. So you use the formula for resistance in parallel:
ω, but you must meet the condition, resistance in parallel be equal to 3 ω. So you use the formula for resistance in parallel:
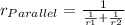 or
or
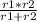
the first way:
you replaces the values for
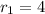 ω and
ω and
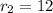 ω in the formula for resistance in parallel and solve the operation:
ω in the formula for resistance in parallel and solve the operation:
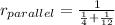

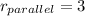 ω
ω
the second way:


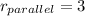 ω
ω
and you got it, the student has getting four values of resistance by using
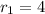 ω and
ω and
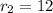 ω and making series and parallel.
ω and making series and parallel.