Question

PLEASE HELP!

One of the reactions for rusting iron is as follows: 4Fe + 3O2 → 2Fe2O3
(MM Fe: 55.85 g/mol; MM O2=32 g/mol; MM Fe2O3=159.70 g/mol)

If 63.98 g of oxygen gas is completely consumed, how many moles of iron (III) oxide are formed?

A. 1.333 mol
B. 3071 mol
C. 2.999 mol
D. 6812 mol

Answer 1

Answer: A. 1.333 mol

Step-by-step explanation:

`4Fe+3O_2\rightarrow 2Fe_2O_3`

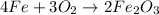
To calculate the moles, we use the equation:

`\text{Number of moles}=\frac{\text{Given mass}}{\text {Molar mass}}`

`\text{Number of moles}=(63.98g)/(32g/mol)=2.0moles`

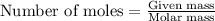
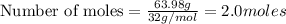
As oxygen is completely consumed, it is the limiting reagent and will limit the formation of
`Fe_2O_3`.

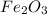According to stochiometry,

3 mole of
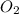`O_2` produces 2 moles of
`Fe_2O_3`

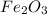
Thus 2 moles of
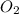`O_2` will produce=
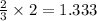`(2)/(3)* 2= 1.333` moles of
`Fe_2O_3`

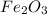
Thus the correct answer is 1.333 moles

Answer 2

he balanced equation for the reaction is
4Fe + 3O₂ ---> 2Fe₂O₃
stoichiometry of O₂ to Fe₂O₃ is 3:2

number of O₂ moles used up - mass present / molar mass of O₂
number of O₂ moles = 63.98 g / 32 g/mol = 1.999 mol

if 3 mol of O₂ forms 2 mol of Fe₂O₃
then 1.999 mol of O₂ forms - 2/3 x 1.999 mol = 1.333 mol
answer is A) 1.333 mol of Fe₂O₃ are formed