Question

2x - y = 5

x + 3y = 7

What is the value of the system determinant?

5
6
7
2. One number is 7 more than twice another. If their difference is 22, what is the larger number?29  37   43

Answer 1

#1) The system determinant is 7. #2) The value of the larger number is 37.

Step-by-step explanation:
For #1): We find the determinant of the coefficient matrix. This is given in a 2x2 matrix with the first row being the coefficient of x and the coefficient of y from the first equation, and the second row being the coefficient of x and the coefficient of y from the second equation:


`\left[\begin{array}{cc}2&-1\\1&3\end{array}\right]`

To find the determinant, find the cross products; multiply 2*3 (6) and -1*1 (-1).

Subtract the cross products: 6- -1 = 6+1 = 7.

For #2): The first equation would be y=2x+7. The second equation would be y-x=22. We will use subsittution to solve this; plug in 2x+7 for y in the second equation, which gives us 2x+7-x=22.

Combine like terms and we have x+7=22.

Subtract 7 from both sides:
x+7-7=22-7
x=15.

Plug this back into the first equation: y=2*15+7=30+7=37.

Answer 2

Question 1:
For this case we have the following system of equations:
2x - y = 5
x + 3y = 7
We rewrite the system of equations of the form:
Ax = b
Where,
A: coefficient matrix.
x: incognita vector
b: vector solution.
We have then:

`A = \left[\begin{array}{ccc}2&-1\\1&3\\\end{array}\right] b = \left[\begin{array}{ccc}5\\7\\\end{array}\right] x = \left[\begin{array}{ccc}x\\y\\\end{array}\right]`
We look for the determinant of A.
We have then:

`A = (2) * (3) - (-1) * (1) A = 6 + 1 A = 7`
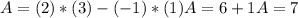Amswer:
the value of the system determinant is:
A = 7

Question 2:
For this case, the first thing we must do is define variables:
x, y: unknown numbers.
We then have the following system of equations:
One number is 7 more than twice another:

`y = 2x + 7`
their difference is 22:

`y - x = 22`
Solving the system of equations we have:

`x = 15 y = 37`
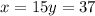
Therefore, the largest number is:

`y = 37`
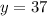Answer:
the larger number is 37