Question

A plastic sun visor allows light to pass through but reduces the intensity of the light. the intensity is reduced by 5% if the plastic is 1mm thick each additional millimetre of thickness reduces the intensity by another 5%

Use an equation to model the relation between the thickness of the plastic and the intensity of light

How thick is a piece of plastic that reduced the intensity of light to 60%

Answer 1

all you gotta do is search up the answer on google instead of brainy. O

Answer 2

Answer: The equation is f(x) =
`0.95^(x)`;

The piece of plastic has to have 10mm of thickness.

Explanation: It is known that with 1 mm of thickness, 5% of the intensity is reduced. So, 95% of the light is transmitted.

For each milimetre added, "more" 95% of light is transmitted.

For example, if another milimetre of plastic is added, another 0.95 of light is transmitted:

0.95.0.95 = 0.9025 of light reach the visor

So, the model that relate thickness of plastic and intensity of light is:

f(x) =
`0.95^(x)`

in which:

f(x) is the intensity of light;

x is thickness in mm;

Using the equation, the thickness necessary to reduce intensity to 60% is:

f(x) =
`0.95^(x)`

0.6 =
`0.95^(x)`

log 0.6 = log
`0.95^(x)`

x. log (0.95) = log (0.6)

x =
`(log 0.6)/(log 0.95)`

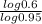
x = 9.95

x ≈ 10

The thickness necessary to reduce intensity of light to 60% is 10mm.