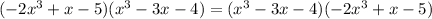Question

Please answer!

What is the product of -2x^3+x-5 and x^3-3x-4?

(A) Show your work.

(B) Is the product of -2x^3+x-5 and x^3-3x-4 equal to the product of x^3-3x-4 and -2x^3+x-5? Explain your answer.

Answer 1

`\textsf{A)}\quad -2x^6+7x^4+3x^3-3x^2+11x+20`

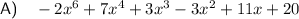
B) Yes → Commutative Law

Explanation:

Part (A)

To find the product of the given quadratic expressions, place each expression in brackets then multiply them:

`\implies (-2x^3+x-5)(x^3-3x-4)`

Distribute the parentheses:

`\implies -2x^3(x^3)-2x^3(-3x)-2x^3(-4)+x(x^3)+x(-3x)+x(-4)-5(x^3)-5(-3x)-5(-4)`

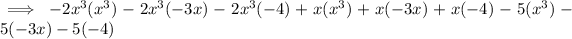
Simplify:

`\implies -2x^6+6x^4+8x^3+x^4-3x^2-4x-5x^3+15x+20`

Group like terms:

`\implies -2x^6+6x^4+x^4+8x^3-5x^3-3x^2-4x+15x+20`

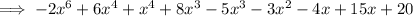
Combine like terms:

`\implies -2x^6+7x^4+3x^3-3x^2+11x+20`

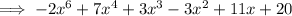
Part (B)

According the to Commutative Law (for multiplication) changing the order or position of two numbers does not change the end result.

`\textsf{Commutative Law}: \quad a \cdot b = b \cdot a`

Therefore:

`(-2x^3+x-5)(x^3-3x-4)=(x^3-3x-4)(-2x^3+x-5)`