Question

Which of the following ordered pairs could be placed in the table below and still have the relation qualify as a linear function? Input (x) Output (y) −5 7 −3 15 −1 23 ? ? (0, 31) (−7, 30) (1, 31) (0, −1)

Answer 1

y increases by 8 as x increases by 2 so the relationship is linear with slope 4. That is y=4x+c and 7=-20+c, so c=27.
The relationship seems to be y=4x+27. The only point to fit this equation is (1,31), Answer 3

Answer 2

The correct option is 3.

Explanation:

If a linear function passing through two point, then the equation of linear function is

`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`

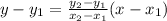
From the given table it is clear that the function passing through the points (-5,7), (-3,15) and (-1,23).

Consider any two points from them, i.e., (-3,15) and (-1,23). So, the equation of line is

`y-15=(23-15)/(-1-(-3))(x-(-3))`

`y-15=(8)/(2)(x+3)`

`y-15=4(x+3)`

`y-15=4x+12`

`y=4x+12+15`

`y=4x+27`

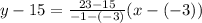
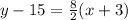
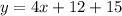
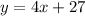
The equation of line is y=4x+27.

At x=0,

`y=4(0)+27=27`

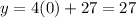
At x=-7,

`y=4(-7)+27=-1`

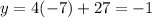
At x=1,

`y=4(1)+27=31`

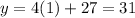
Only point (1,31) is satisfy the equation of line. Therefore the ordered pairs (1,31) could be placed in the table below and still have the relation qualify as a linear function.

Hence option 3 is correct.