Answer:
The value of the x is 176.6 cm .
Explanation:
By using the pythagorean theorem .
Hypotenuse² = Perpendicular² + Base²
As in the ΔTVY .
TV² = VY² + YT²
As TV= 95.2 cm
VY = 34 cm
Putting the values in the above
95.2² = 34² + YT²
9063.04 - 1156 = YT²
7907.04 = YT²
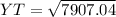
YT = 88.9 cm (Approx)
As in the ΔTYK .
TK² = KY² + YT²
TK = 168 cm
TY= 88.9 cm
Putting the values in the above
168² = 88.9² + YK²
28224 - 7903.21 = YK²
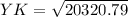
YK = 142.6 cm (Approx)
Thus
VK = VY + YK
Putting the values in the above
VK = 34 + 142.6
= 176.6 cm
Therefore the value of the x is 176.6 cm .