Question

Three security cameras were mounted at the corners of a triangular parking lot. camera 1 was 158 ft from camera 2, which was 121 ft from camera 3. cameras 1 and 3 were 140 ft apart. which camera had to cover the greatest angle?

Answer 1

This is a good exercise to apply the law of cosines and the law of sines:
First, we are going to use the law of cosines to find any angle, and then we can use the law of sines to find the other one; last but not least we are going to use the internal angles definition (the sum of the interior angles of a triangle is 180°) to fin our final angle and compare them:

Using the law of cosines: we know that
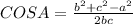
`COSA= (b^(2)+ c^(2)- a^(2) )/(2bc)`, but we need the vale of the angle A, so we are going to use the inverse cosine function, ARCCOS, to solve for A:

`A=ARCCOS((b^(2)+ c^(2)- a^(2) )/(2bc))`
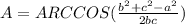
We also know that a=121, b=140, and c=158, so the only thing we have to do is replace the values into our equation:

`A=ARCCOS((140^(2)+ 158^(2)- 121^(2) )/(2(140)(158)))`

`A=ARCCOS( (29923)/(44240))`

`A=47.4`°

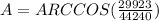
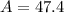
Now that we know the value of the angle A, we can use the law of sines to find the angle B:

`(SinA)/(a) = (SinB)/(b)`

`SinB= (bSinA)/(a)`
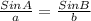
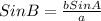
And just like before we'll use the inverse sine function, ARCSIN, to solve for B:

`B:ARCSin( (bSinA)/(a) )`
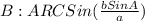
We know that b=140, a=121, and A=47.4, so we can replace the vales to get:

`B=ARCSin( (140Sin(47.4))/(121) )`

`B=58.4`°

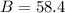
Now that we have two angles, we can use the interior angle definition. If the sum of the interiors angle of a triangle is 180°, then:

`C=180-(A+B)`

`C=180-(47.4+58.4)`

`C=108-105.8`

`C=74.2`

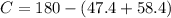
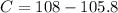
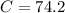
We can conclude that the camera that has to cover the greatest angle is camera 3, and it has to cover an angle of 74.2°.