Question

The voltage drop across the resistor is the product of the (constant) resistance r of the resistor, and the current i(t) passing through the resistor. the voltage drop across a capacitor is equal to q c , where q(t) is the charge on the capacitor, and the constant c is the capacitance of the capacitor. across a voltage source (typically a battery or a power supply), the voltage increases by v(t) , so the voltage drop is is −v(t) . the current passing through the resistor and the charge on the capacitor are related by the equation i = dq/dt . write a differential equation for the charge q(t) on the capacitor as a function of time. your answer should depend on q, v , and the constants r and c , but not on i . in your answer, write just q and v for the functions q(t) and v(t) . remember to insert a space or explicitly type "*" between two letters to indicate multiplication.

Answer 1

Okay, so using Kirchhoff's Loop Rule, we know the voltage drop across the entire system is 0. We can model this in a equation.

Vbatt = Vcap + Vres.

We are also told the voltage drop across the capacitor is I(t)R and voltage drop across the capacitor is q(t)/C. We can then substitute dq/dt in for I(t). We get:

Vbatt = q(t)/C + (dq/dt)R

This gets rid of the problem of I. Now we just have to get dq/dt by itself.

V - q/C = (dq/dt)*R Subtract q/C
(1/R)*(V - q/C) = dq/dt Divide by R on both sides


`(dq)/(dt) = (1)/(R)(V - (q)/(C) )`

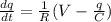
I think this is right, but don't quote me.
Hope this helps!