Question

37​% of adults say cashews are their favorite kind of nut. You randomly select 12 adults and ask each to name his or her favorite nut. Find the probability that the number who say cashews are their favorite nut is​ (a) exactly​ three, (b) at least​ four, and​ (c) at most two. If​ convenient, use technology to find the probabilities.

Answer 1

It is given that about 37% of the adults say cashew nuts are their favorite nut. And a sample of 12 adults are taken to name their favorite nut.

We note that probability of
`$x$` successes out of
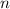`$n$` trial is given by :

`$P(n,x)=^nC_x p^x (1-p)^((n-x))$`

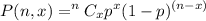
Here, number of trails, n = 12

probability of success, p = 0.37

number of successes, x = 3

a). Therefore the probability of the adults to say cashew nut as their favorite of exactly three is given by :

`$P(3)=^(12)C_3 (0.37)^3 (1-0.37)^((12-3))$`

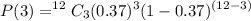
= 0.174217909

b). We know that :

P(at least x) = 1 - P(at most x - 1)

So we use the cumulative binomial distribution table.

i.e.
`$P(x \geq 4) = 1 -P(x \leq3)$`

`$= -1[P(x=0)+P(x=1)+P(x=2)+P(x=3)]$`

`$= 1-[^(12)C_0 (0.37)^0 (0.63)^(12)+^(12)C_1 (0.37)^1(0.63)^(11)+^(12)C_2 (0.37)^2(0.63)^(10)+^(12)C_3(0.37)^3(0.63)^9]$`= 0.70533

Therefore, P(at least 4) = 0.70533

c).
`$P(x \leq 2) = P(x=0) + P(x=1)+P(x=2)$`

`$=^(12)C_0(0.37)^0(0.63)^(12)+^(12)C_1(0.37)^1(0.63)^(11)+^(12)C_2(0.37)^2(0.63)^(10)$`

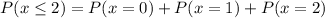
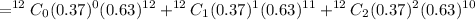
= 0.12045205

Therefore, P(at most 2) = 0.12045205