Question

Michelle asked her father how old he is. “Guess”, the father answered. “If you add the digits that make my age this year, you’ll get a number three times bigger than if you do it next year.” How old is the father?

Answer 1

He is 39 because 3+9=12, and next year he would be 40. 4+0=4, and 12 is 3 times larger than 4. He's old.

Answer 2

we are given that

“If you add the digits that make my age this year, you’ll get a number three times bigger than if you do it next year.”

Let the first digit of the father's age be x and the second digit be y

Then we can write

`x+y= 3(x + y + 1) \\ \\ x+y= 3(x + y) + 3\\`

`3(x+y)-(x+y)=-3\\ \\ 2(x+y)=-3\\ \\ (x+y)=-3/2\\ \\`

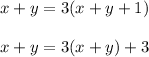
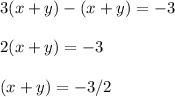
Since
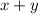`x + y` cannot be negative,

So we can again write

`x + y = 3(x + 1 + y - 9) \\ \\ x+y= 3(x + y - 8) \\ \\ x+y= 3(x + y) - 24`

`2(x+y)=24\\ \\ x+y=12\\`

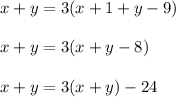
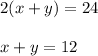
Hence age of the father is 39.