Answer:
 inches.
inches.
Explanation:
Length of first ribbon
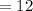 inches.
inches.
Length of second ribbon
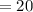 inches.
inches.
To find the greatest length he can make of smaller strips that are all equal in length, we need to find the H.C.F of the two numbers.
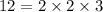
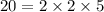
For H.C.F, we will take the product of all the common factors in the prime factorization of the two numbers.
H.C.F

So, he can cut three
 inches ribbons from the
inches ribbons from the
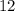 inches ribbon and five
inches ribbon and five
 inches ribbons from the
inches ribbons from the
 inches ribbon.
inches ribbon.
Hence, the greatest length he can make of smaller strips that are all equal in length is
 inches.
inches.