Question

Find the probability that a randomly selected student has a score between 60 and 100Find the probability that a randomly selected student has a score between 60 and 100

Answer 1

The answer is below

Explanation:

The question is not complete let us assume a mean of 80 and a standard deviation of 10.

The z score is a score used in statistics to determine by how many standard deviations the raw score is above or below the mean. The z score is given by:

`z=(x-\mu)/(\sigma) \\\\where\ \mu=mean, \sigma=standard\ deviation\\\\for\ a\ sample\ size(n):\\\\z=(x-\mu)/(\sigma/√(n) ) \\\\`

Given that μ = 80, σ = 10

For x = 60:

`z=(x-\mu)/(\sigma) =(60-80)/(10)=-2\\ \\\\\\`

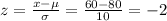
For x = 100:

`z=(x-\mu)/(\sigma)=(100-80)/(10)=2\\\\ \\\\`

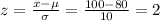
Therefore from the normal distribution table, P(60 < x < 100) = P(-2 < z < 2) = P(z < 2) - P(z < -2) = 0.9772 - 0.0228 = 0.9544