1) Function:
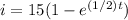
2) Average = [value of the function a t = 0 + value of the function at t = 4 ] / 2
3) Value of the function at t = 0
15[1 - e^(0) ] = 15 [ 1 - 1] = 0
4) Value of the function at t = 4
15 [ 1 - e^ (4/2) ] = 15 [ 1 - e^(2) ]
5) Average
{ 0 + 15 [1 - e ^ (2) ] } / 2 = 7.5 [ 1 - e^(2)]
Given that all the options show e raised to negative 2, I guess you made a mistake on the function.