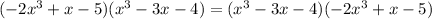Answer:
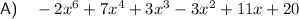
B) Yes → Commutative Law
Explanation:
Part (A)
To find the product of the given quadratic expressions, place each expression in brackets then multiply them:

Distribute the parentheses:
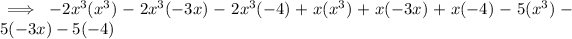
Simplify:
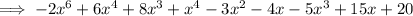
Group like terms:
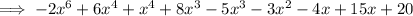
Combine like terms:
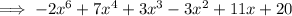
Part (B)
According the to Commutative Law (for multiplication) changing the order or position of two numbers does not change the end result.

Therefore: