Question

the library at a certain University reported the journal prices had increased by 150% over a period of 10 years The report concluded that this representing a price increase of 15% each year if journal prices had indeed increase by 15% each year what percentage increase would that give the over 10 years Ron your answer as a percentage to the nearest whole number

Answer 1

1.15¹⁰=4.0456, the growth rate, so the increase is 3.0456 or 305%.

Answer 2

Over 10 years, increasing 15% each year, the prices would have increased 305%.

Explanation:

If journal prices had a constant rate of increase, it's prices could be modeled by the following equation:

`P(t) = P(0)(1+r)^(t)`

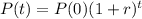
In which P(t) is the price after t years, P(0) is the initial price and r is the rate of increase.

If it increased 15% each year.

We would have r = 0.15. So

`P(t) = P(0)(1.15)^(t)`

Over 10 years

`P(10) = P(0)(1.15)^(10)`

`P(t) = 4.05P(0)`

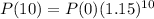
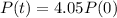
The initial price is 100%

4.05P(0) - P(0) = 3.05P(0)

Over 10 years, increasing 15% each year, the prices would have increased 305%.