Answer:
The total distance used by Ted was 10 miles, uphill and downhill.
Explanation:
Givens:
- Uphill hike:
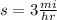 ;
;
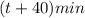
- Downhill:
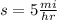 ;
;

So, Ted climbs the same distance in both directions, because it's the same trajectory, but at different speeds:
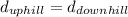
Applying the definition of a constant movement:
 , we have:
, we have:
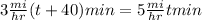
However, we first need to transform the time in hours, because the speed is using hours in its unit. So, we know that 1 hour equals 60 minutes:
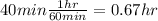
Therefore, the equation will be:
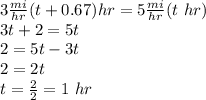
Therefore, downhill we took 1 hour, and uphill he took 1.67 hr or 1 hr and 40 min.
Now, we use this time to find the length of Ted's hike.
Uphill:
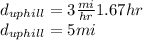
Downhill:

Therefore, the total distance used by Ted was 10 miles, uphill and downhill.