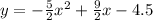Answer:
The equation of parabola is
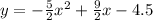 .
.
Explanation:
Equation of a parabola is quadratic equation.
Let the equation of parabola be
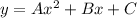 .... (1)
.... (1)
The parabola contains points ( -2, -23.5), (0,-4.5), (4,-26.5).
Put (0,-4.5) in equation (1),
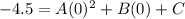
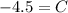
Put this value in equation (1).
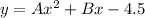 ... (2)
... (2)
Put ( -2, -23.5) and (4,-26.5) in equation (2).
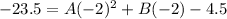
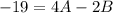 .... (3)
.... (3)
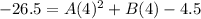
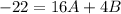 .... (4)
.... (4)
On solving (3) and (4), we get
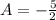 and
and
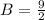
Therefore the value of parabola is