Answer:
3.79 m/s²
Step-by-step explanation:
Given that:
The mass of refrigerator = 120 kg
The height of refrigerator = 2.20 m
The width of refrigerator = 85.0 cm = 0.85 m
Since the center of gravity is located at the geometrical center.
Then;
the center mass of refrigerator = h/2 = 2.20 m / 2
= 1.10 m
From width of refrigerator, the distance of center mass to either edge of refrigerator = 0.85 m / 2
= 0.425 m
So; the torque acting on the center mass due to the force F is:
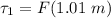
the torque acting on the center mass due to the weight of the refrigerator is:
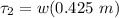
Thus, since the refrigerator does not tip over,

F(1.10 m) = w(0.425 m)
ma (1.10 m) = mg (0.425 m)
a (1.10 m) = g(0.425 m)
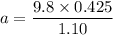
a = 3.79 m/s²