Answer:
AD= 6 ft
Explanation:
We have given that : In a right triangle ΔABC, the length of leg AC = 5 ft and the hypotenuse AB = 13 ft
To find : The length of angle bisector of angle A
Solution : Since, ΔABC is a right angle triangle
applying Pythagoras theorem, we can find the length of side BC
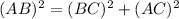
⇒
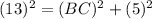
⇒
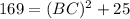
⇒
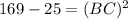
⇒
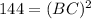
⇒ BC=12
Now, we find the ∠A
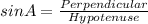
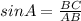
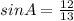
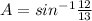
∠A=67.38°
Now, we have given that A is the angle bisector on BC at pt. D
which means it divide angle into two equal parts
Therefore, ∠A'= ∠A /2= 67.38/2= 33.69°
Now, In ΔCAD
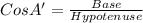
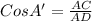


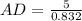
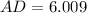
Therefore, the length of the angle bisector of ∠A = AD≈ 6 ft