Question

A conical wine glass has the dimensions shown. if the wine is poured into a cylindrical glass of the same diameter, how high will it rise?​

Answer 1

The bowl of glass 1 is cylindrical. The inside diameter is 5 cm and the inside height is 6 cm.

The bowl of glass 2 is composed of a hemisphere attached to cylinder. The inside diameter of both the hemisphere and the cylinder is 6 cm. The height of the cylinder is 3 cm.

The bowl of glass 3 is an inverted cone. The inside diameter is 6 cm and the inside slant height is 6 cm.

Answer 2

The wine will rise to a height of approximately 2.87 cm in the cylindrical glass.

To find the height to which the wine will rise in the cylindrical glass, we can use the concept of volumes.

The volume of a cone is given by the formula:

`V_(cone) = (1)/(3) \pi r^2h_(cone)`

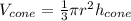
​The volume of a cylinder is given by the formula:

`V_(cylinder) =\pi r^2 h_(cylinder)`

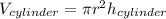
​Given that the conical wine glass has a height (
`h_(cone)`) of 8.6 cm and a radius (r) of 1.3 cm, we can use these values to find the volume of the cone.

`V_(cone) = (1)/(3) \pi (1.3^2 )(8.6)`

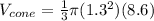
Next, we can set the volume of the cone equal to the volume of the cylindrical glass, and solve for the height (
`h_(cylinder)` ) of the cylindrical glass.

`(1)/(3) \pi (1.3^2 )(8.6)=\pi (1.3^2 )h_(cylinder)`

​Cancel out common terms:

`(1)/(3) (8.6)=h_(cylinder)`

`h_(cylinder) = (8.6)/(3)`

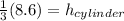
Now, calculate the value:

`h_(cylinder) =2.8667`

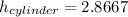
Therefore, the wine will rise to a height of approximately 2.87 cm in the cylindrical glass.