Question

What is the square root of 2

Answer 1

`√(2)` is, well,
`√(2)`. It's what's called an irrational number, which means that it can't be written as the ratio of two integers (i.e. numbers like 3/5, 8/13, 256/689), though I might as well take this time to go into one of my favorite proofs. I'm going to show you why it's impossible to write
`√(2)` as a fraction, and we're going to start by assuming that it is possible.

Proof:
`√(2)` is irrational.

Assume
`√(2)` is rational. If
`√(2)` is rational, it must be able to be written as the ratio of two integers - let's call them p and q -
`(p)/(q)`. Let's assume that
`(p)/(q)` is in simplest form; we can't reduce it any more.

We know that
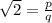
`√(2)= (p)/(q)`, which means that, squaring both sides:


`2 = \big( (p)/(q)\big)^2`


`2= (p^2)/(q^2)`

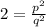
Multiplying both sides by
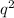
`q^2`, our equation becomes:


`2q^2=p^2`

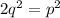
Since this shows that
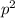
`p^2` is a multiple of 2, we know that p is even, since squaring it gives us another even number.

Any even number is just 2 multiplied by some integer - let's call that integer k - so we can say that, since p is even:


`p = 2k`

Plugging that back in, we get:


`2q^2=(2k)^2`

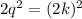
Expanding the right side:


`2q^2=4k^2`

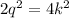
And dividing both sides by 2:


`q^2 = 2k^2`

So
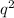
`q^2` is even, which means that q is even, too. But wait, what did we say at the beginning?

"Let's assume that
`(p)/(q)` is in simplest form; we can't reduce it any more."

But, since both p and q are even, we can reduce our fraction by dividing p and q by 2, so we just contradicted ourselves! Since we assumed something was true, and following a completely logical set of steps made it come out false, we know that our assumption was wrong! So,


`√(2)` is irrational.

End of story. Or, as mathematicians tend to say it, Q.E.D. (Quod erat demonstrandum - "which was to be demonstrated")