Answer: The value of x = 48°.
Explanation:
Since we have given that
O is the center of the circle and PA and PB are two tangents.
Angle at the center = ∠AOB = 132°
We need to find the value of x .
Since Radius forms right angle at the tangents as it is the shortest distance from the center to the tangent.
So, ∠PAO= 90°
∠PBO = 90°
since it forms a quadrilateral,
So, we know that " Sum of all angles in the quadrilateral is 360°. "
So, we have
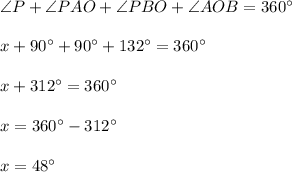
Hence, the value of x = 48°.