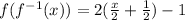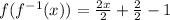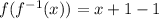Question

What is the inverse of the function
f(x)=2x+1

Answer 1

`f^(-1)(x)=(x)/(2)+(1)/(2).`

Explanation:

As we have a lineal function, there is a easy way to find the inverse
`f^(-1)(x)`:

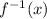First, switch the x and y, that is if we have

y = f(x) = 2x-1, then after the change we obtain

x = 2y-1.

Then, clear y:

`x = 2y-1`

`x+1 = 2y`

`(x+1)/(2) = y`

`(x)/(2)+(1)/(2) = y.`

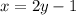
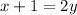
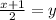
Then,
`f^(-1)(x)=(x)/(2)+(1)/(2)` is the inverse of y=2x-1.

You can check it composing both functions, if you obtain x the inverse is correct.

`f(f^(-1)(x))= 2((x)/(2)+(1)/(2))-1`

`f(f^(-1)(x)) = (2x)/(2)+(2)/(2)-1`

`f(f^(-1)(x)) = x+1-1`

`f(f^(-1)(x)) = x.`

Answer 2

Inverses are easy for this problem. First we start with the equation. Then we change the f(x) to y to make this whole problem easier.
y=2x+1
Isolate the x and solve for x.
x=(y-1/2)
Switch x and y again.
y=(x-1/2)
Add function notation.
f^-1(x)=(x-1/2)
Done! And if you need to check if equations are inverses, add the original equation into the x variable of the inverse. The solution should be f^-1(x)=x. That means the inverse is right.