Question

Enter the explicit rule for the sequence

Answer 1

Let's take a look at the first few numbers in the sequence based on the given rule:


`a_(1)=6\\ a_(2)= (1)/(4)(6)\\ a_3= (1)/(4)\big( (1)/(4)\big)6= \big((1)/(4)\big)^2(6)\\ a_(4)= (1)/(4) \big((1)/(4)\big)^26= \big((1)/(4)\big)^3(6)`

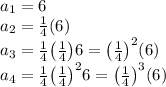
Inspecting this pattern it seems like the power
`(1)/(4)` is being raised to is always one less than the number of the sequence, so if we were on the nth number in the sequence, that part of the expression would be
`\big((1)/(4) \big)^(n-1)`. We also know that we'll be multiplying whatever we get from that by 6, so we can write the full explicit rule for our sequence as


`a_n=6\big( (1)/(4) \big)^(n-1)`

Where
`a_n` is the nth number in our sequence.