Answer:
The probability is about 60%
Explanation:
Given a circle is inscribed in an equilateral triangle.
A point in the figure is selected at random then we have to find its probability.
Let the radius of circle is r and side of equilateral triangle is a
OD=r
As centroid of the triangle divides the median into 2:1
∴ AO=2r
In ΔABD,


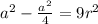
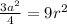
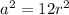
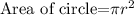

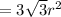
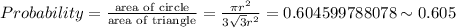
In percentage:
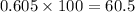
which is about 60%
Hence, the correct option is A.