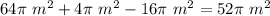Question

Find the area of the shaded regions. Give your answer as a completely simplified exact value in terms of π (no approximations)

Answer 1

Do you know how to find the area of a circle?
Find the area of the biggest circle, subtract the area of the unshaded circle, then add the area of the smallest circle.

Answer 2

`52 \pi\ m^(2)`

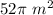
Explanation:

we know that

The area of the shaded regions is equal to the area of the larger circle plus the area of the smaller circle minus the area of the unshaded circle

Remember that

The area of the circle is equal to

`A=\pi r^(2)`

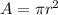
Step 1

Find the area of the larger circle

we have

`r=8\ m`

substitute

`A=\pi (8)^(2)=64 \pi\ m^(2)`

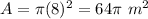
Step 2

Find the area of the smaller circle

we have that

`OB=OP`

so

`AB=OB/2`

`AB=8/2=4\ m`

`r=4/2=2\ m`

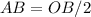
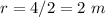
substitute

`A=\pi (2)^(2)=4 \pi\ m^(2)`

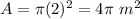
Step 3

Find the area of the unshaded circle

we have that

`OB=OP`

so

`AO=OB/2`

`AO=8/2=4\ m`

`r=4\ m`

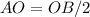
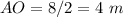
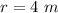
substitute

`A=\pi (4)^(2)=16 \pi\ m^(2)`

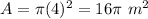
Step 4

Find the area of the shaded regions

`64 \pi\ m^(2)+4 \pi\ m^(2)-16 \pi\ m^(2)=52 \pi\ m^(2)`