Answer:
The monthly payment is $316.54.
Explanation:
It is given that Charlotte purchased a pool for $7680. The rate of interest is 20.45%.
She use a six-month deferred payment plan with an interest rate of 20.45%.
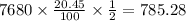
The principle amount after six-month deferred payment is
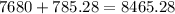
![PV=C* [(1-(1+r)^(-n))/(r)]](https://img.qammunity.org/2019/formulas/mathematics/high-school/j279e86s339kls3uywj9vqp3uin7mddwjs.png)
Where, PV is present value, C is monthly payment, r is rate of interest and n is number of years.
![8465.28=C* [(1-(1+((0.2045)/(12))^(-36))/((0.2045)/(12))]](https://img.qammunity.org/2019/formulas/mathematics/high-school/7iudyndvqmckmz46er23l5voccv50kwb0l.png)
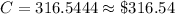
Therefore the monthly payment is $316.54.