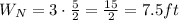Question

(05.01)A poster is shown below: A rectangle is shown. The length of the rectangle is labeled 12 feet. The width of the rectangle is labeled 3 feet. What are the dimensions if the poster is enlarged by a factor of five over two ? 7.5 ft by 30 ft 15 ft by 60 ft 1.5 ft by 6 ft 15 ft by 6 ft

Answer 1

The correct answer is the first option: 7.5 ft by 30 ft.

Explanation:

If a rectangle is enlarged by a certain factor, that means that its height and width are both enlarged by such a factor. The new dimensions of the rectangle are obtained by multiplying the old dimensions by the enlarging factor, therefor we can compute the new dimensions as:

`W_N = W_O \cdot f`

`H_N = H_O \cdot f`

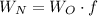
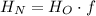
Where
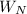`W_N` is the new width,
`W_O` is the old width,
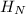`H_N` is the new height,
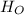`H_O` is the old height, and
`f` is the enlarging factor.

From the above we can finally get that:

`W_N = 3 \cdot (5)/(2) = (15)/(2) = 7.5 ft`

`H_N = 12 \cdot (5)/(2) = (60)/(2) = 30 ft`

Answer 2

Option A) 7.5 ft by 30 ft

Explanation:

We are given the following information:

Dimension of rectangle:

Length = 12 feet

Width = 3 feet

The poster is enlarged by a factor of
`(5)/(2)`

After enlargement, we can write

`\text{Enlarged length} = \text{Original length}* \text{Factor}\\\text{Length of Poster} = \text{Length of Rectangle}* \displaystyle(5)/(2)\\\\\text{Length of Poster} = (12* 5)/(2) = (60)/(2) = 30\text{ feet}\\\\\text{Width of Poster} = \text{Width of Rectangle}* \displaystyle(5)/(2)\\\\\text{Width of Poster} = (3* 5)/(2) = (15)/(2) = 7.5\text{ feet}`

The dimension of poster is 7.5 feet by 30 feet

Option A) 7.5 ft by 30 ft