Question

A 12.9 kg pelican, with a 1.51 kg fish in its mouth, is flying 14.94 m/s at a height of 114 m when the fish wiggles free and fall back toward the ocean. How fast is the fish moving when it hits the water

Answer 1

v = 49.6 m/s

Step-by-step explanation:

The vertical component of the final speed can be found by using 3rd equation of motion:

`2gh = v_(y)^(2) - v_(0y)^(2)\\`

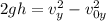
where,

g = acceleration due to gravity = 9.81 m/s²

h = height = 114 m

Voy = vetical component of initial velocity = 0 m/s (since the pelican is flying horizontally)

Vy = Vertical component of final velocity = ?

Therefore,

`(2)(9.81\ m/s^(2))(114\ m) = v_(y)^(2) - (0\ m/s)^(2)\\v_(y) = \sqrt{2236.68\ m^(2)/s^(2)}\\v_(y) = 47.3\ m/s`

Now, the horizontal component of the velocity is assumed to be the same because of negligible frictional force. Therefore,

Vx = 14.94 m/s

Thus the final speed will be given as:

`v = \sqrt{v_(x)^(2) + v_(y)^(2)}\\\\v = \sqrt{(14.94\ m/s)^(2) + (47.3\ m/s)^(2)}\\\\`

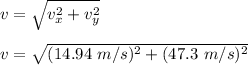
v = 49.6 m/s