Question

Given z1 = 2(cos 60° + i sin 60°) and z2 = 8(cos 150° + i sin 150°), what is z1z2?

3(cos 210° + i sin 210°)
3(cos 90° + i sin 90°)
16(cos 210° + i sin 210°)
16(cos 90° + i sin 90°)

Answer 1

Answer: Choice C

`16\left(\cos 210^(\circ) +i\sin 210^(\circ) \right)`

=========================================================

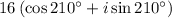
Step-by-step explanation:

If

`\text{z}_1 = r_1*\text{cis}(\theta_1) \ \text{ and } \ \text{z}_2 = r_2*\text{cis}(\theta_2)`

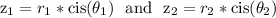
then

`\text{z}_1*\text{z}_2 = (r_1*r_2)*\text{cis}(\theta_1+\theta_2)`

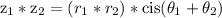
We multiply the r values and add the theta values.

The cis is shorthand for "cosine i sine"

• c = cosine
• i = imaginary number equal to
  `√(-1)`
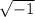
• s = sine

It's useful to shorten something like
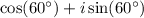`\cos(60^(\circ))+i\sin(60^(\circ))` into
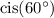`\text{cis}(60^(\circ))` so we don't have to do too much tedious busy-work of writing the same long string over and over. It also makes the formula above much nicer to handle.

---------------------------

We are given these complex numbers in polar form

`\text{z}_1 = r_1*\text{cis}(\theta_1) = 2*\text{cis}(60^(\circ))\\\\\text{z}_2 = r_2*\text{cis}(\theta_2) = 8*\text{cis}(150^(\circ))\\\\`
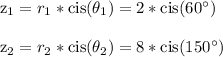
The r values 2 and 8 multiply to 2*8 = 16

The theta values add to 60+150 = 210

Therefore,

`\text{z}_1*\text{z}_2 = (r_1*r_2)*\text{cis}(\theta_1+\theta_2)\\\\\text{z}_1*\text{z}_2 = (2*8)*\text{cis}(60^(\circ)+150^(\circ))\\\\\text{z}_1*\text{z}_2 = 16\text{cis}(210^(\circ))\\\\\text{z}_1*\text{z}_2 = 16\left(\cos(210^(\circ))+i\sin(210^(\circ))\right)\\\\`

This points us to choice C as the final answer.

-----------------------

Geometric interpretation of what's going on: Multiplying complex numbers means we apply a scaling and rotation.

The scaling part is multiplying the r values together. This indicates we're moving further away from the origin.

The rotation is where we add the angles together.

Multiplying complex numbers is useful in applications such as physics and computer graphics (such as CGI in movies or videogames) where vectors are used all the time. There are many other useful applications as well.