Answer: Choice C
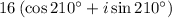
=========================================================
Step-by-step explanation:
If
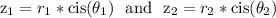
then
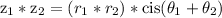
We multiply the r values and add the theta values.
The cis is shorthand for "cosine i sine"
- c = cosine
- i = imaginary number equal to
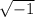
- s = sine
It's useful to shorten something like
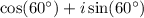 into
into
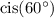 so we don't have to do too much tedious busy-work of writing the same long string over and over. It also makes the formula above much nicer to handle.
so we don't have to do too much tedious busy-work of writing the same long string over and over. It also makes the formula above much nicer to handle.
---------------------------
We are given these complex numbers in polar form
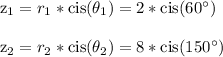
The r values 2 and 8 multiply to 2*8 = 16
The theta values add to 60+150 = 210
Therefore,
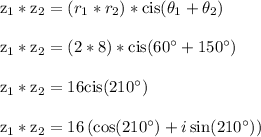
This points us to choice C as the final answer.
-----------------------
Geometric interpretation of what's going on: Multiplying complex numbers means we apply a scaling and rotation.
The scaling part is multiplying the r values together. This indicates we're moving further away from the origin.
The rotation is where we add the angles together.
Multiplying complex numbers is useful in applications such as physics and computer graphics (such as CGI in movies or videogames) where vectors are used all the time. There are many other useful applications as well.