Question

A bacteria population is 6000 at time t = 0 and its rate of growth is 1000 · 9t bacteria per hour after t hours. what is the population after one hour? (round your answer to the nearest whole number.)

Answer 1

14384

Explanation:

We are given that

P(0)=6000

`(dP)/(dt)=1000\cdot 9^t`

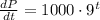
We have to find the population after 1 hour.

`dP=1000(9^t)dt`

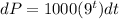
Taking integration on both sides

`P=1000\int 9^t dt`

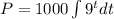
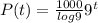`P(t)=(1000)/(log 9)9^t`+C

Using formula:
`\int a^t=(1)/(log a)a^t+C`

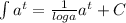
Substitute t=0 and P(0)=6000

`6000=(1000)/(log9)+C`

`C=6000-(1000)/(log 9)=6000-(1000)/(0.954)`

`C=4952`

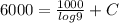
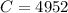
Substitute the values then we get

`P(t)=1047.95(9^t)+4952`

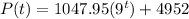
Substitute t=1

Then, we get

`P(1)=1047.95(9)+4952`

`P(1)=14384`

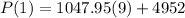
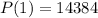
Hence, the population after one hour=14384

Answer 2

dP/dt = 1000 * 9^t is the bacteria population's growth rate.where:P(t) is the population at time t, andP(0) = 6000.
The population after one hour would be:
P(1) = P(0) + <Integral of dP/dt from 0 to 1>
P(1) = P(0) + [ 1000 * 9^1 / ln(9) - 1000 * 9^0 / ln(9) ]
P(1) = 6000 + 3641 = 9461 would be the answer