Question

Identify the transformation that maps the regular hexagon with a center (-7, 3.5) onto itself

Answer 1

the answer is D , because you rotate 120 degrees  clockwise 

Answer 2

Option D - rotate 120° clockwise about (-7, 3.5) and reflect across the line x=-7

Explanation:

To identify : The transformation that maps the regular hexagon with a center (-7, 3.5) onto itself

Solution :

A regular hexagon which has 6 axes of symmetry.

So, the angle of rotational symmetry is given by 360 divides by number of sides.

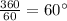`(360)/(60)=60^\circ` is the angle of rotational symmetry.

Since 90° is not a multiple of 60°, we will eliminate choices A and B.

120° is a multiple of 60°

So, it rotate clockwise 120°

Reflection across the line :

When you reflect a point across the line y = x, the x-coordinate and y-coordinate change places.

Which implies that the reflection across the line is x=-7

Therefore, Option D is correct that the transformation of a regular hexagon is

rotate 120° clockwise about (-7, 3.5) and reflect across the line x=-7