Question

PLEASE HELP! I'M ON A TIMER

A rope is swinging in such a way that the length of the arc traced by a knot at its bottom end is decreasing geometrically. If the third arc is 18 ft. long and the seventh arc is 8 ft. long, what is the length of the arc on the sixth swing? Round your answer to the nearest tenth of a foot.

Answer 1

Length of the arc on the sixth swing = 9.80 ft

Step-by-step explanation:

A rope is swinging in such a way that the length of the arc traced by a knot at its bottom end is decreasing geometrically.

Length of 3rd arc = 18 ft

Length of 7th arc = 8 ft

We have to find the length of arc formed in a the 6th swing.

As we know in a geometric sequence, explicit formula is given as

`a_(n)=a(r)^(n-1)`

where
`a_(n)` is the nth term, a is the first term, r is the common ratio and n is the number of term

Now for 3rd term of the sequence ⇒
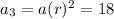`a_(3)=a(r)^(2)=18`------(1)

For 7th term of the sequence ⇒
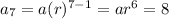`a_(7)=a(r)^(7-1)=ar^(6)=8` ------(2)

Now we divide equation 2 from equation 2

`(a_(7))/(a_(3) )=(a.r^(6))/(a.r^(2))=(8)/(18)`

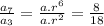
we solve it further

`r^(4)=(4)/(9)`

`r^(2)=\sqrt{(4)/(9)}=(2)/(3)`

`r=\sqrt{(2)/(3)}=√(0.667)=0.817`

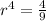
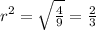
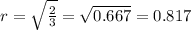
Now we put the value of r in equation 1

a.r² = 18

a.(√0.667)²= 18

a×0.667 = 18 ⇒ a = 26.986

Now we will calculate the 6th term of this sequence

`a_(6)=(26.99).(0.0.817)^(6-1)=(26.99)(0.817)^(5)=(26.99).(0.363)=9.80`

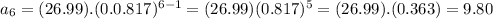
Answer is Length of the arc on the 6th swing = 9.80 ft

Answer 2

The correct answer is 9.8 ft.

Step-by-step explanation:
This is a geometric sequence, which follows the explicit formula

`g_n=g_1* r^(n-1)`

where g₁ is the first term, r is the common ratio and n is the term number.

We know that the third term is 18; this gives us 18=g₁×r³⁻¹ or 18=g₁×r².

We also know the seventh term is 8, which gives us 8=g₁×r⁷⁻¹ or 8=g₁×r⁶.

Solving for g₁ in the third term gives us g₁=18/r², and solving for g₁ in the seventh term gives us g₁=8/r⁶. They both equal g₁ so we set them equal to each other:

18/r² = 8/r⁶.
Multiply both sides by r⁶, which gives us
18r⁶/r² = 8.

Using our properties of exponents, we have 18r⁴ = 8. Divide both sides by 18, which gives us
r⁴=8/18.

We can find the fourth root by taking the square root twice:
taking the square root gives us r² = √8/√18.

Simplifying √8 we get 2√2, and simplifying √18 gives us 3√2; we now have

r²=2√2)/3√2.

The √2 will cancel, leaving r²=2/3. Taking the square root again, we have

r=√2/√3; simplifying this gives us r=√6/3.

We can now work backward to find the sixth term using the seventh one; Divide 8 by √6/3. Dividing by a fraction means multiplying by the reciprocal, so we multiply 8 by 3/√6; this gives us 24/√6, and in a calculator that gives us 9.8 ft.