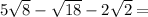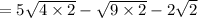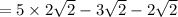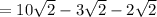You have sqrt(8), sqrt(18), and sqrt(2).
You need to simplify the radicals.
sqrt(2) is already simplified.
For both sqrt(8) and sqrt(18), you need to factor out the greatest perfect square.
8 = 4 * 2
You can take the square root of 4 and put it outside the root.
18 = 9 * 2
You can take the square root of 9 and put it outside the root.